Derivation of Backpropagation in Convolutional Neural Network (CNN)

Introduction

The backpropagation algorithm has emerged as a highly successful method for training complex Neural Network models like Convolutional Neural Networks (CNNs) with greater ease. Despite the computational challenges associated with training Deep Neural Networks, backpropagation provides the possibility for training these networks in the first place. Convolutional Neural Network (CNN) as we know is one of the ideal Neural Network architectures for Image Processing and Recognition. However, the way CNNs learn through backpropagation differs from traditional neural networks. In this article, we will delve deep into the process of performing the backpropagation (backward pass) on different layers in Convolutional Neural Networks. We will explore the complete derivation, and mathematical concepts involved. Let's get started. 

The Forward Pass In CNN

Typically, Neural Networks have two phases, one is the Forward pass where the inputs are passed through the network for producing output, and the backpropagation is where the gradients of error are passed from right to left for training the network. Before diving into the intricacies of backpropagation, we need to understand how a forward pass is done. Well, we have an entire article about all sorts of basics about CNN including Forward Pass, It is highly recommended to check it. You can refer to it here.

Forward Pass in Convolution Layer

CNN, architecture

Convolutional Neural Networks (CNN) have different layers starting from Convolution, Pooling, Flattening, and Fully Connected. The Forward Pass starts from the Convolutional Layer where there are two things to note, one is the input image and the other is the filter or kernel.  Now, a kernel or filter is also known as a feature detector which is a set of weights that holds some of the most important features in the input image. A Convolution operation is performed on this layer with the input image and the kernels, then the resulting output also known as a feature map is obtained,

The mathematical form of this operation looks like this,

 \[(I * K)(i,j)  = \sum^m_{i=1} \sum^n_{j=1} (I_{(i+m-1)(j+n-1)} \star rot180(K_{ij})) + b_i\]

A lot of stuff going around here. There is no problem for us to visualize 2D in our brain apart from 4D or 5D. So, if you visualize the 2D shape of the image and kernel in your brain and how they can be applied, things are really simple. The \(I\) is our input or we can say a 2-dimensional image and the \(K\) is the Kernel which is also 2D. What about the indices? The \(i, j\) are indices that are used to represent a single pixel in the input image, kernel, and the produced output. \(m, n\) are used to represent the dimensions (height, width) of the filter or kernel. The, \(I_{(i+m-1)(j+n-1)}\) represents the specific pixel value of the input image at the position \((i+m-1, j+n-1)\). As \(i\) and \(j\) change, the filter is applied through each of the input pixels. Now, there are two sums, and the outer summation \(\sum^m_{i=1}\) is used to slide the kernel over the input image which iterates over \(i\) from 0 to \(m-1\) slides vertically over the input image. Meanwhile, the inner summation \(\sum^n_{j=1}\) is used for element-wise multiplication which iterates over \(j\) from 0 to \(n-1\), representing the horizontal sliding of the kernel over the image. Finally, a bias term \(b_i\) is added for providing flexibility for the network.

But what about this term \(rot180(K_{ij})\)? This term says to rotate the kernel 180 degrees before element-wise multiplication is applied. But why do we need to do this? This brings us to a fundamental question, are we applying Convolution or Cross-Correlation? For that, you need to understand the difference between Convolution and Cross-Correlation.

Difference between Convolution and Cross-Correlation

The difference between cross-correlation and convolution in mathematics seems small and even is considered negligible, but it is important when comes to the derivations in CNN. In most cases, when we consider an input and a kernel matrix and directly perform the operation that we consider a convolution, it is not actually a convolution operation, but a cross-correlation operation. The simple difference is that in cross-correlation, you just do the element-wise multiplication by sliding the kernel over the input matrix without any modification, but in order to become a convolution operation, you need to flip the kernel 180 degrees and do the same. So, basically, Convolution is the cross-correlation operation applied to an Image matrix and a 180-degree rotated Kernel matrix.

Here is how we can visually understand it,

Convolution vs Cross-Correlation

This animation shows the difference between cross-correlation and convolution. You might also notice the symbol difference, the symbol for cross-correlation is \(\star\) while the symbol for convolution is \(*\).

So, intuitively, the concept of discussing cross-correlation might seem meaningless, instead, we can directly discuss convolution. But, during the derivation, you may often see this thing \(rot180(K_{ij})\), at that time you can simply recall that convolution is the operation of cross-correlation applied on a flipped kernel. 

Forward Pass in Pooling Layer

Alright, we have got a feature map after convolving the input image and kernel, now the next process is to apply pooling which is done on the pooling layer,

What happens in the Pooling Layer is very simple and straightforward. In the case of Max Pooling, a window slides over the input feature map, and the maximum value within each window is selected as the output. From the obtained feature map let's perform the Max Pooling operation,

\[ (I * K)(i,j) = \begin{bmatrix} 23 & 14 & 25 \\ 27&  29& 35 \\ \end{bmatrix}\]

When applying max-pooling of shape 2x2, we'll get,

\[MaxPool((I*K)(i,j))= \begin{bmatrix} max(23, 14, 27, 29) & max(14, 25, 29, 35) \\ \end{bmatrix}\]

\[MaxPool((I*K)(i,j))=\begin{bmatrix} 29 & 35 \\ \end{bmatrix}\]

Forward Pass in Flattening

Now, the flattening layer, here the output obtained from Convolution and Pooling is transformed into a one-dimensional vector so that it can be passed to the Dense or Fully Connected layer. Since our output obtained is already one-dimensional let's consider another example,

\[MaxPool((I*K)(i,j))= \begin{bmatrix} 1 & 3 & 5 \\ -4 & 0 & -3 \\ 5 & 7 & -9 \\ \end{bmatrix}\]

When this matrix is flattened it will look like this,

\[F = \begin{bmatrix} 1 & 3 &  5& -4 & 0 & -3 & 5 & 7 & -9 \\ \end{bmatrix}\]

Forward Pass in Fully Connected Layer

A full connection layer is something the same as a Multi-Layer Perceptron (MLP). In a Fully Connected Layer, each neuron is connected to every neuron in the previous layer, forming a fully interconnected network. The term "Fully Connected" is specifically used in CNNs to distinguish it from other layers we have discussed. Unlike convolutional and pooling layers that share weights across inputs, the Fully Connected Layer assigns unique weights to each input value.

The forward pass on each neuron of the Fully Connected Layer is simple as this,

\[output = \Phi (W_{ij} . X_{j} + b_{j})\]

Where, W = Weights and X = inputs from the preceding layer, Φ = Activation function. This equation is simple and we have learned it when starting the basics of Neural Networks. Here we are computing the weighted sum of inputs, and adding a bias.

Here is a simple animation that shows how the forward pass is done in CNN,

Convolution, Pooling, Fattening, Dense

Backpropagation in CNN

Now comes the most important part of this article, we are starting to discuss how backpropagation is done in Convolutional Neural Networks. So you have familiar with the forward pass now, the backward pass or backpropagation is nothing but doing the reverse of the forward pass where we find the gradient of each of the neuron with respect to the loss function to determine how much the output contribute to the overall loss. In Forward Pass, we start from the Convolution Layer until the Fully Connected Layer, In backpropagation, we start from the Fully Connected Layer all the way up to the Convolution Layer.

Backpropagation Through the Fully Connected (Dense) layer.

The first step is to find a Loss Function which is used to evaluate the output produced from the output layer of the Dense network. The choice of the Loss function completely depends on which task you want the network to do. Things get different in binary, multiclass, and regression problems. For illustration, Let's consider Binary Cross Entropy loss here,

Derivative of Binary Cross Entropy

\[L(y, \hat{y}) = - \frac{1}{n} \sum_{i=1}^n (y_i) \text{log}(\hat{y_i}) + (1-y_{i})log(1-\hat{y_{i}})\]

The binary cross-entropy loss function finds the dissimilarity between the predicted probability and the true binary label. 

Binary Cross Entropy loss calculation

The derivative of Loss with respect to \(\hat{y_i}\) when applying chain rule,

\[\begin{align} \frac{\partial{L}}{\partial{\hat{y_i}}} = \frac{\partial}{\partial{\hat{y}_i}}(- \frac{1}{n} \sum_{i=1}^n (y_i) \text{log}(\hat{y_i}) + (1-y_{i})log(1-\hat{y_{i}})) \\ = \frac{\partial{}}{\partial{\hat{y_i}}}(-\frac{1}{n}(y_i \text{log}(\hat{y_i})) + \frac{\partial}{\partial{\hat{y_i}}}((1-y_i)\text{log}(1-\hat{y_i}))) \\ = -\frac{1}{n}\left(\frac{{y_i}}{{\hat{y}_i}} - \frac{{1-y_i}}{{1-\hat{y}_i}}\right) \tag{1} \end{align}\]

Derivative of loss with respect to weights

That's the derivation of Binary Cross Entropy, Now the next thing we need to do is to find how much the changes in weights affect the loss function \(\frac{\partial L}{\partial w_{ij}}\), which helps to find the gradient of loss with respect to weights.

For deriving how the weights affect the overall loss function in the output layer, you will need to take into account two things, how much the output affects the loss and how much the weights affect the output. This is what we call the chain rule,

\[\frac{\partial{L}}{\partial{w_{ij}}} = \frac{\partial{L}}{\partial{\hat{y_i}}}.\frac{\partial{\hat{y_i}}}{\partial{w_{ij}}}\]

We know that, 

\[\begin{align} \hat{y_i} = x_{j}.w_{ij} + b_j \end{align}\]

So we can simplify \(\frac{\partial{\hat{y_i}}}{\partial{w_{ij}}}\),

\[\begin{align} \frac{\partial{\hat{y_i}}}{\partial{w_{ij}}} = \frac{\partial}{\partial{w_{ij}}} \left ( x_{j}.w_{ij} + b_j \right ) \\ \frac{\partial}{\partial{w_{ij}}}\left ( x_{j}.w_{ij} \right ) \\ \frac{\partial{w_{ij}}}{\partial{w_{ij}}}.x_j \\ = x_j \end{align}\]

So \(\frac{\partial{L}}{\partial{w_{ij}}}\) becomes,

\[\begin{align} \frac{\partial{L}}{\partial{w_{ij}}} = \frac{\partial{L}}{\partial{\hat{y_i}}}.x_j \\ = -\frac{1}{n}\left(\frac{{y_i}}{{\hat{y}_i}} - \frac{{1-y_i}}{{1-\hat{y}_i}}\right) . x_j \tag{2} \end{align}\]

This is the equation for finding the gradient of loss with respect to weights,

Derivative of loss with respect to inputs

Next, let's find the gradient of the loss with respect to inputs, ie, how much the change in inputs affects the loss, note that the inputs to one corresponding layer are the output coming from the previous layer, and that's the whole thing about backpropagation, to pass the gradients of inputs backward. This illustration can be seen in the image shown. Using the chain rule, we can calculate this.

The change in loss with respect to input is influenced by the weights and the change in loss with respect to the outputs. Here is how we can represent it,

\[\frac{\partial L}{\partial x_j} = \sum_{i=1}^{n} \frac{\partial L}{\partial{\hat{y_i}}}.w_{ij}\]

Which can be also denoted as, 

\[-\frac{1}{n} \sum_{i=1}^{n} \left(\frac{{y_i}}{{\hat{y}_i}} - \frac{{1-y_i}}{{1-\hat{y}_i}}\right).w_{ij} \tag{3}\]

Derivative of loss with respect to bias

Finally, we need to find the gradient of loss with respect to bias, \(\frac{\partial L}{\partial b_j}\). Using the chain rule we can find that, 

\[\frac{\partial L}{\partial b_j} = \frac{\partial{L}}{\partial{\hat{y_i}}}.\frac{\partial \hat{y_i}}{\partial b_j}\]

This represents how much the loss changes with respect to the outputs, and how much the output changes with respect to the bias. Using the same idea for input gradient calculation, we can find the value of \(\frac{\partial \hat{y_i}}{\partial b_j}\)

\[\begin{align}\frac{\partial \hat{y_i}}{\partial b_j} = \frac{\partial}{\partial b_j}\left ( x_j.w_{ij} + b_j \right ), \text{where} \text{  } \hat{y_i} = x_{j}.w_{ij} + b_j \\ \frac{\partial b_j}{\partial b_j} = 1 \end{align}\]

Which means,

\[\frac{\partial L}{\partial b_j} = \frac{\partial{L}}{\partial{\hat{y_i}}} \tag{3}\]

Updating weights & bias using Gradient Descent

Ok, the calculations are done and we find the gradients, the next and most important step in backpropagation is to update the weights and bias using the gradients of weights and bias. Here is how the weights and bias can be updated,

Updating weights:

\[\begin{align} w_{ij}^{new} = w_{ij}^{old} - \eta \cdot \frac{\partial L}{\partial w_{ij}} \\ \\ =  w_{ij}^{old} + \eta \cdot \frac{1}{n}\left(\frac{{y_i}}{{\hat{y}_i}} - \frac{{1-y_i}}{{1-\hat{y}_i}}\right) . x_j \end{align}\]

where \(\eta\) is the learning rate, \(w_{ij}^{new}\) is the newly updated weights, \(w_{ij}^{old}\) is the old weights, and \( \frac{\partial L}{\partial w_{ij}}\) is the gradient of loss with respect to weights,

Updating bias:

\[b_j^\text{new} = b_j^\text{old} - \eta \cdot \frac{\partial L}{\partial b_j} \\ b_j^\text{old} + \eta \cdot \frac{1}{n} \left(\frac{y_i}{\hat{y}_i} - \frac{1-y_i}{1-\hat{y}_i}\right) \]

where \(\eta\) is the learning rate, \(b_{j}^{new}\) is the newly updated bias, \(b_{j}^{old}\) is the old bias, and \( \frac{\partial L}{\partial b_{j}}\) is the gradient of loss with respect to bias,

So we have completed the calculation of finding the gradients and updating the weights of the Fully Connected Layer of the CNN. Note that it is not only the case of the output layer, for each layer, including the output layer, the same set of equations is used to compute the gradients and updated the parameters. This involves applying the chain rule and differentiating the loss function with respect to the layer's parameters, such as weights and biases, as well as with respect to the layer's inputs.

Backpropagation Through MaxPooling Layer

When going backward, the next layer after the Dense Layer is a Pooling Layer. So the next step is to pass the gradients of inputs produced from the Dense layer to the Pooling Layer. But, between the Dense and Pooling layers, there is one more layer called the Reshape Layer. 

The Reshape Layer

When comes to the forward pass, we usually convert the 2D outputs after Pooling them into a 1D vector to apply it to a Dense Layer since the Dense layer deal with vector inputs. So in the backward pass, we need to reverse this process, which is to convert the 1D gradient vector from the Dense Layer to a 2D gradient matrix for Pooling and Convolutional Layers.

The process of reshaping in the backward pass can be determined based on the shape of the pooling layers in the forward pass. The specific shape of the pooling layers will determine how the 1D gradient vector from the Dense layer should be transformed back into a 2D gradient matrix.

When considering Max-Pooling or Pooling in general, you need to note that there is no actual gradient calculation done, instead, passing the gradient backward according to the Pooling function used. 

In the case of Max Pooling, you will select the maximum value from each window and produce the output in the forward pass, In backpropagation, the gradient corresponding to the maximum values is sent backward and the rest is considered as 0.

Here is the representation of how the backpropagation is done on the Max Pooling Layer,

\[\begin{align} \frac{\partial L}{\partial x_{ij}} = \frac{\partial L}{\partial{\hat{y_{ij}}}}.\delta _{ij} \\ \\  \delta_{ij} = \begin{cases} 1 & \text{if } \text{max pooling location} \\ 0 & \text{otherwise}\end{cases}\end{align}\]

What does this all mean? Here \(\delta_{ij}\) is called a mask or switch variable which is used to switch between 1 and 0 for different positions in the 2D gradient matrix. If the value became 1, then the gradient is passed backward and if the value became 0, then the gradient is not passed. The value became 1 on those positions where the maximum values are found and the rest of them are zero. Just do the reverse of Max Pooling.

So that's all that happens in Pooling Layer during training using the backpropagation algorithm, This process is similar to any pooling function but the operation completely depends on which pooling function you are using.

Backpropagation Through the Convolution Layer

Indeed, after covering the previous stages, we have now arrived at the final stage: the Convolutional Layer. An interesting observation is that the backward derivations for the Dense Layer and Convolutional Layer share certain similarities. The only difference is that here we apply Convolution rather than dot product operation. 

Similar to the Dense Layer, we need to find the gradients with respect to weights, inputs, and bias. However, there are a few key differences to note.

Firstly, due to the 2D nature of the convolutional layer, we require three indices to track the dimensions. These indices include the indices for the height and width of the kernel, input image, and output, and then the index used to track the position of the kernel in the input image.

Secondly, instead of performing a dot product as in the Dense layer, the convolutional layer applies a convolution operation. This operation involves sliding a kernel or filter over the input matrix and computing element-wise multiplications and summations.

Lastly, in the discussion so far, we have considered a single convolution. However, in a typical CNN, multiple convolutions are applied, each with its own set of weights and output feature map. In such cases, additional indices would be necessary to keep track of these convolutions. If you understand all of this, then things are pretty easy.

Derivative of Loss with respect to weights in Convolution Layer.

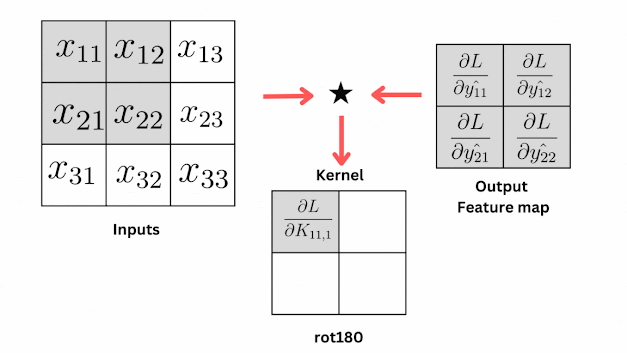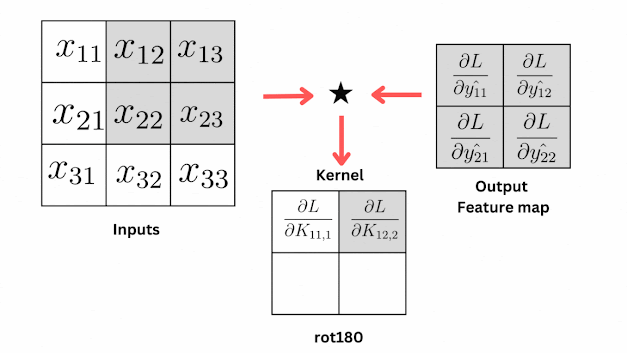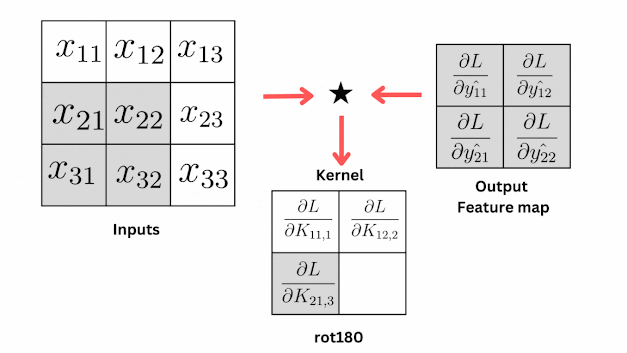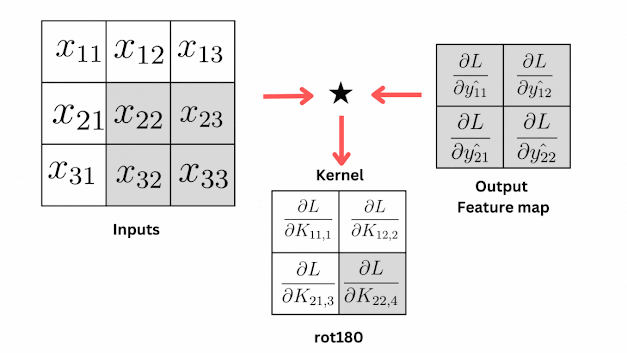Derivative of Loss with respect to weights in Convolution Layer.

From the animation, you can see that the gradients of the kernel are produced by convolving the output feature map and the input matrix.

Here is the equation for finding how much the loss changes with respect to the weights using the chain rule,

\[\begin{align}\frac{\partial L}{\partial K_{ijk}} = \frac{\partial L}{\partial{\hat{y}_{ij}}} \star \frac{\partial{\hat{y}_{ij}}}{{\partial \text{ rot180}(K_{ijk})}} \\ = \frac{\partial L}{\partial{\hat{y_{ij}}}} * x_{ij}\end{align}\]

Now, you can relate the equation and animation, as per the equation the kernel gradients are produced by convolving the gradients in the output matrix and the values in the input matrix.

Remember we have told about cross-correlation and its similarity with convolution, using the same principle we applied the cross-correlation operation here and then the kernel is rotated 180 degrees.

Derivative of Loss with respect to inputs in the Convolution Layer.

Derivative of Loss with respect to inputs in the Convolution Layer.

The change in loss with respect to inputs can be given by,

\[\frac{\partial L}{\partial x_{ij}} = \sum_{i=1}^{m}\sum_{j=1}^{n} \frac{\partial{L}}{\partial{\hat{y_{i,j}}}} \star \text{rot180}(K_{ijk})\]

The change in the loss w.r.t inputs is given by the double summation of the change in loss w.r.t output produced after cross-correlation and the 180-degree rotated kernel. 

Derivative of Loss with respect to bias

Finally, let's see how to calculate the derivative of loss w.r.t bias. it depends on the change in loss with respect to the change in outputs.

\[\frac{\partial{L}}{\partial{b_{j}}} = \sum_{j=1}^{m} \frac{\partial L}{\partial{\hat{y_{ij}}}}\]

That's it, we have derived all the necessary things including the gradients of Kernels, inputs, and bias, now let's update the Kernels and bias using gradient descent.

Updating Kernels and Bias using Gradient Descent

Updating Kernels:

\[K_{ijk}^\text{new} = K_{ijk}^\text{old} - \eta \cdot \frac{{\partial L}}{{\partial K_{ijk}}}\]

Updating bias:

\[b_j^\text{new} = b_j^\text{old} - \eta \cdot \frac{{\partial L}}{{\partial b_j}}\]

Both the derivations of Fully Connected Layer and Convolution Layer seem similar. However, the key difference is the operations and the indices that need to track, if you understand how these things are different when comes from 1D to 2D, then you nailed it!.

Finally, we have done the whole forward and backward derivation of Convolutional Neural Networks. Now a few things you can do, just try to plug the exact derivative value of the loss function into the backward pass calculations in the Convolution layer which help you understand it well.

Thanks for reading!